FINANCIAL OPTIMIZATION SPECIALIST

Revolutionizing Financial Planning Through Advanced Mathematics

Developing cutting-edge portfolio optimization frameworks with AI-driven solutions for complex financial challenges.

View My Work All Projects
Yuhe Sui
ABOUT ME

Mathematical Expertise Applied to Financial Challenges

I'm a mathematics student at Raffles Institution, Singapore, specializing in the application of advanced mathematical concepts to financial modeling and portfolio optimization. My work focuses on leveraging AI and mathematical techniques to solve complex challenges in finance and investment planning.

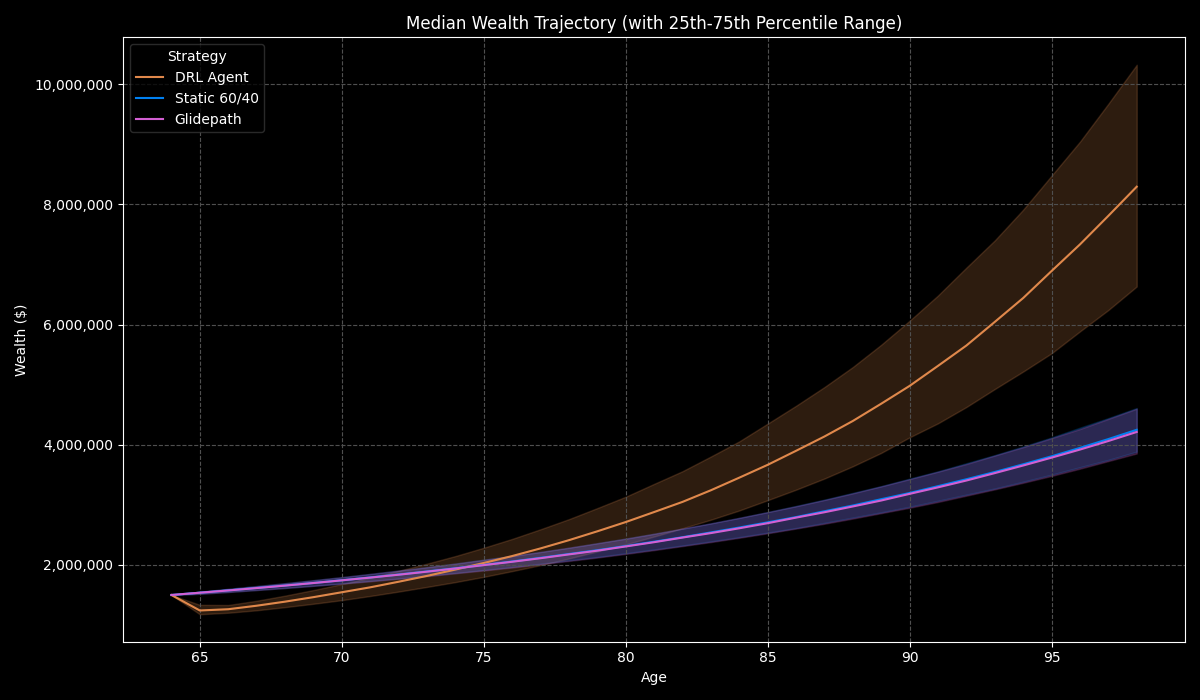
With extensive training in mathematical olympiads and programming, I combine rigorous analytical skills with innovative approaches to develop cutting-edge financial solutions. My recent research explores dynamic multi-objective retirement portfolio optimization using reinforcement learning.

Stanford University

Pre-Collegiate Studies

Raffles Institution

Singapore

Olympiad Training

Mathematics & Physics

Data Analytics

Google Certification

MY EXPERTISE

Financial & Technical Skills

Portfolio Optimization

Creating advanced multi-objective optimization frameworks with dynamic asset allocation strategies.

Financial Modeling

Building sophisticated financial models to simulate market conditions and evaluate investment strategies.

Risk Management

Implementing advanced risk assessment techniques to protect against downside scenarios in portfolios.

Algorithmic Trading

Developing quantitative strategies using mathematical algorithms and machine learning.

Technical Proficiencies

Mathematical Tools

Advanced Calculus 95%
Linear Algebra 90%
Optimization Techniques 92%
Stochastic Processes 85%

Programming & Analytics

Python (NumPy, Pandas) 90%
R & Statistical Analysis 85%
AI/ML for Finance 88%
Data Visualization 92%
FEATURED PROJECT

DMO RetPortfolio+

AI-Powered Retirement Portfolio Optimization

The Challenge

Developing a comprehensive retirement portfolio framework for aging populations facing complex financial risks: downside market risk, longevity risk, and healthcare cost uncertainty.

The Solution

Created a multi-objective optimization model using deep reinforcement learning that dynamically adjusts portfolio allocation based on changing market conditions and health status.

  • AI-driven dynamic asset allocation with real-time adaptation
  • Health trajectory modeling integrated with financial planning
  • Advanced risk mitigation strategies with superior downside protection
  • Portfolio rebalancing algorithms that adapt to market volatility
Deep Reinforcement Learning LSTM Networks Python Financial Modeling Risk Assessment
View Full Case Study View All Projects
DMO RetPortfolio+ Project

Key Results

Portfolio Value

2× Higher

vs traditional strategies

Healthcare Coverage

16.7% OOP

vs 50% with traditional

Longevity Protection

74.7%

annuity adequacy

Quality of Life

19.7 QALYs

maintained throughout

My Journey

Education

2023 - 2024

Raffles Institution

GCE A Levels - Further Mathematics Student

Relevant Coursework: Further Mathematics and Mathematics (Conics, Linear Algebra, Numerical Methods, Differential Equations), Physics (Newtonian Mechanics, Thermodynamics, Electromagnetism, Modern Physics), Economics (Macroeconomics, Microeconomics, International Trade).

Experience & Training

Jun 2024 - Aug 2024

Stanford University

Pre-Collegiate Studies Online

Completed intensive coursework in Mathematical Finance, including advanced applications of stochastic calculus, Monte Carlo simulations, and options pricing models. Developed a comprehensive project on optimizing investment portfolio strategies using machine learning techniques.

Selective Admission Program
Apr 2023 - Nov 2023

Raffles Institution

Mathematical Olympiad Training

Selected for specialized training in advanced mathematical problem-solving techniques. Coursework covered Number Theory, Combinatorics, Geometry, and Algebra at an olympiad level. Trained with past International Mathematical Olympiad (IMO) problems.

Top 5% Selection Criteria
Apr 2023 - Nov 2023

Raffles Institution

Physics Olympiad Training

Participated in rigorous training for physics competitions, covering advanced topics in Mechanics, Thermodynamics, Electromagnetism, and Modern Physics. Developed strong analytical and experimental skills through laboratory work and theoretical problem-solving.

Selective Admission Program
Dec 2021 - Jun 2022

Coursera

Google Data Analytics Specialization

Completed comprehensive data analytics curriculum covering data preparation, processing, analysis, and visualization. Developed proficiency in SQL, R, and Tableau. Completed case studies on data-driven decision making and trend analysis for business applications.

Professional Certification
RECOGNITION

Awards & Achievements

Mathematics Excellence

2023

Shanghai TI Cup Math Contest

Achieved Level 1 Award, ranking in the top 5% nationally, demonstrating exceptional mathematical problem-solving abilities.

Top 5% Nationally
2023

American Mathematics Contest 12B

Earned Certificate of Distinction, placing in the top 5% of participants in this prestigious international competition.

Distinction (Top 5%)
2022

Singapore & Asian Schools Math Olympiad

Received Gold Award, ranking 11th in Singapore, showcasing exceptional performance among top mathematics students across Asia.

Gold Award (11th in SG)
2022

Singapore Mathematical Olympiad

Awarded Silver Medal for outstanding problem-solving skills in Singapore's premier national mathematics competition.

Silver Medal

Computing & Data Science

2024

USA Computing Olympiad (USACO)

Advanced to Silver Division, demonstrating strong algorithmic thinking and programming skills in this prestigious competition.

Silver Award
2023

USA Computing Olympiad (USACO)

Earned Bronze Division qualification, showcasing fundamental computational problem-solving abilities.

Bronze Award
2022

Singapore Junior Physics Olympiad

Received Honorable Mention for outstanding performance in physics problem-solving and theoretical concepts.

Honorable Mention

Creative Design

2023

Texas Instruments Graphing Calculators

Awarded Bronze for innovative design and algorithm implementation using graphing calculator technology.

Bronze Award
2019

3D Creative Design Competition

Recognized with Second Class Honors for exemplary 3D design work, demonstrating creative problem-solving and technical execution.

Second Class Honors
GET IN TOUCH

Let's Connect

Contact Information

Phone

+65 98995965

School Email

[email protected]

Send Me a Message